Theory

In numerical analysis and scientific computing, the backward Euler method (or implicit Euler method) is one of the most basic numerical methods for the solution of ordinary differential equations. It is similar to the (standard) Euler method, but differs in that it is an implicit method. The backward Euler method has error of order one in time(Wikipedia).

Implementation and Plots

Now let us see the implementation of explict euler formula using python.

"""
It takes partition boundaries-"a,b", the differential equation-"F", initial values-'c', and the step size-'h'
as argument and returns the numerical solution.
"""
def euler_implict(a, b, F, c, h):
  N = int((b-a)/h + 1)
  t = np.linspace(a, b, N)
  y = np.zeros((len(t), len(c0)))
  y[0] = c
  for k in range(N):
    f1 = lambda  : x - y[k] - h*F(x, t[k+1])
    y[k+1] = fsolve(f1, y[k])
  return y

Example

  1. Write code to solve the following system of ordinary differential equations

Subject to the initial conditions

  1. The exact solution of the above system of ODEs is given by

Let us implement the above system of ode and compire with the exact solution by plotting.

Import libraries

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
from scipy.integrate import odeint
import warnings
warnings.simplefilter("ignore")

Define the exact solutions

x1t = lambda t : np.exp(-t*0.5) # exact solution for x2
x2t = lambda t : -2*np.exp(-t*0.5) + 3*np.exp(-t*0.25) # exact solution for x2
x3t = lambda t: 1.5*np.exp(-t*0.5) - 9*np.exp(-t*0.25) + 8.5*np.exp(-t*1/6) # exact solution for x3

Define the system of the differential equation

# defining the system of the differential equation
def model(x, t):
    x1, x2, x3 = x
    dx1dt = -0.5*x1 # for x1
    dx2dt = 0.5*x1 - 0.25*x2 # for x2
    dx3dt = 0.25*x2 - (1/6)*x3 # for x3
    return np.array([dx1dt, dx2dt, dx3dt])

Assigne the values of the parametrs and call our function.

a, b = [0, 4] # boundaries
h = 0.01 # step size
c = np.array([1, 1, 1]) # the intitial values
eu = euler_implict(model, x0, t) # call the function
eu1_im = eu[:,0] # solution for x1
eu2_im = eu[:,1] # solution for x2
eu3_im = eu[:,2] # solution for x3

#### plot
Let us define a function to plot the solutions and the error.
```python 
def plot(time, exact, approximate, label, title, abs_er):
    
    # plot for exact vs approximation
    plt.figure(figsize=(16, 4))
    plt.subplot(1,2,1)
    plt.plot(time, exact, linewidth = 8, label="Exact")
    plt.plot(time, approximate, linewidth = 6, linestyle='--', label=label)
    plt.xlabel('time')
    plt.ylabel('X')
    plt.title(title)
    plt.legend()
    
    
    # plot for absolute error
    plt.subplot(1,2,2)
    plt.plot(time, abs_er)
    plt.title('Absolute error')
    plt.xlabel('time')
    plt.ylabel("error")

Now let us plot it.

print()
print()
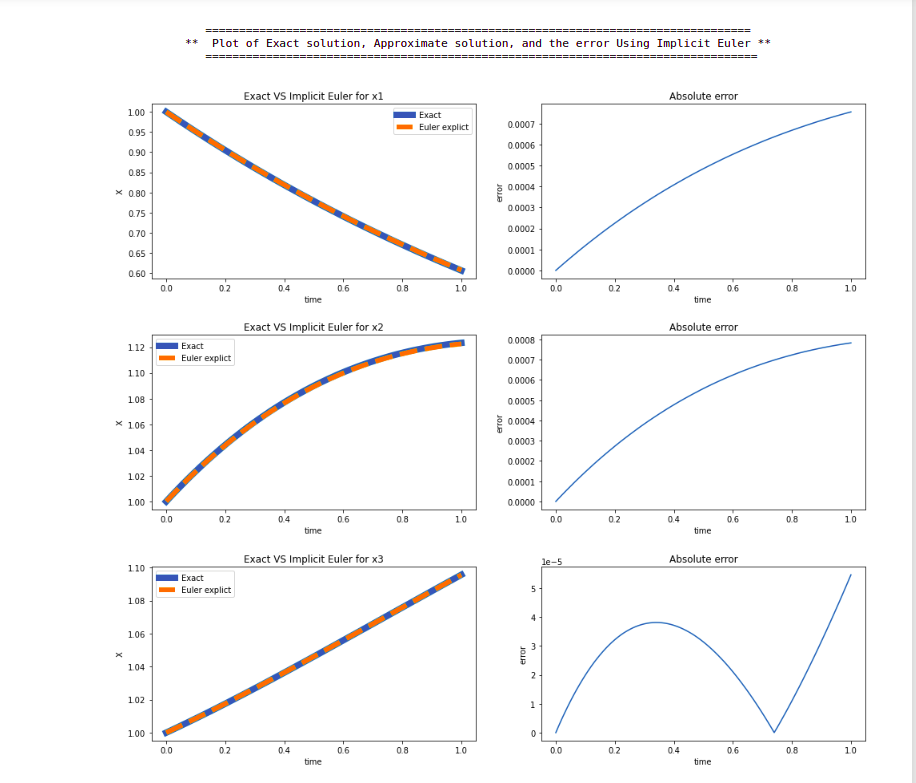
print("\t      =================================================================================")
print(f"\t   **  Plot of Exact solution, Approximate solution, and the error Using Implicit Euler **")
print("\t      ==================================================================================\n")

plot(t, x1t(t), eu1_im, 'Euler explict', "Exact VS Implicit Euler for x1", abs(x1t(t) - eu1_im)) # plot for x1
plot(t, x2t(t), eu2_im, 'Euler explict', "Exact VS Implicit Euler for x2", abs(x2t(t) - eu2_im)) # plot for x2
plot(t, x3t(t), eu3_im, 'Euler explict', "Exact VS Implicit Euler for x3", abs(x3t(t) - eu3_im)) # plot for x3

Implicit Euler